Modelos multinivel

Unidades en contexto
Sesión 4:
Estimación en distintos niveles
- Lectura: Finch cap. 2: Introduction to Multilevel Data Structure
- Práctica 3. Estimación modelos multinivel con lmer en R
Sobre el CONTEXTO
Investigación sociológica y contexto
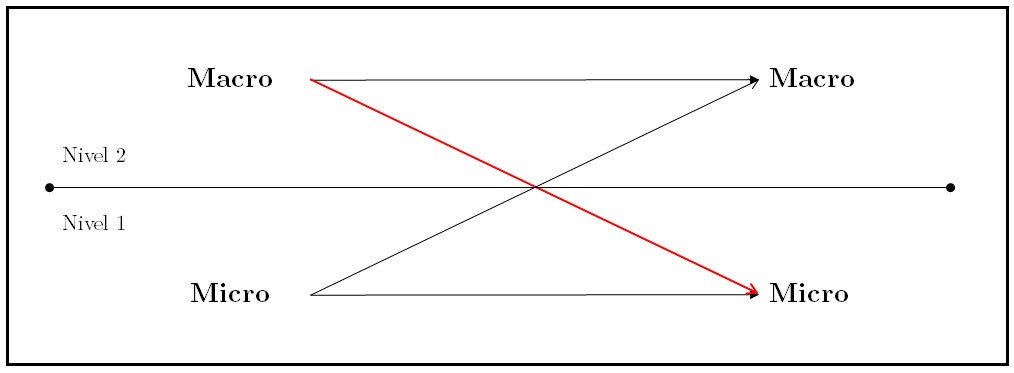
(adaptado de Coleman, 1986)
Datos anidados / con estructura jerárquica
| IDi | IDg | var_i1 | var_i2 | var_g1 | var_g2 |
|---|---|---|---|---|---|
| 1 | 1 | 8 | 7 | 4 | 1 |
| 2 | 1 | 5 | 5 | 4 | 1 |
| 3 | 1 | 3 | 1 | 4 | 1 |
| 4 | 2 | 3 | 2 | 6 | 8 |
| 5 | 2 | 1 | 4 | 6 | 8 |
| 6 | 2 | 7 | 5 | 6 | 8 |
Posibles problemas de inferencia con datos jerarquicos
Problemas asociados a la inferencia y el contexto
Problemas asociados a la inferencia y el contexto
Falacia ecológica:
- Conclusiones erradas acerca de individuos basados en datos de contexto
Problemas asociados a la inferencia y el contexto
Falacia ecológica:
- Conclusiones erradas acerca de individuos basados en datos de contexto
Falacia individualista:
- Conclusiones erradas acerca de contextos basados en datos de individuos
Ejemplo falacia ecológica
Relación entre estatus socioeconómico e intención de voto
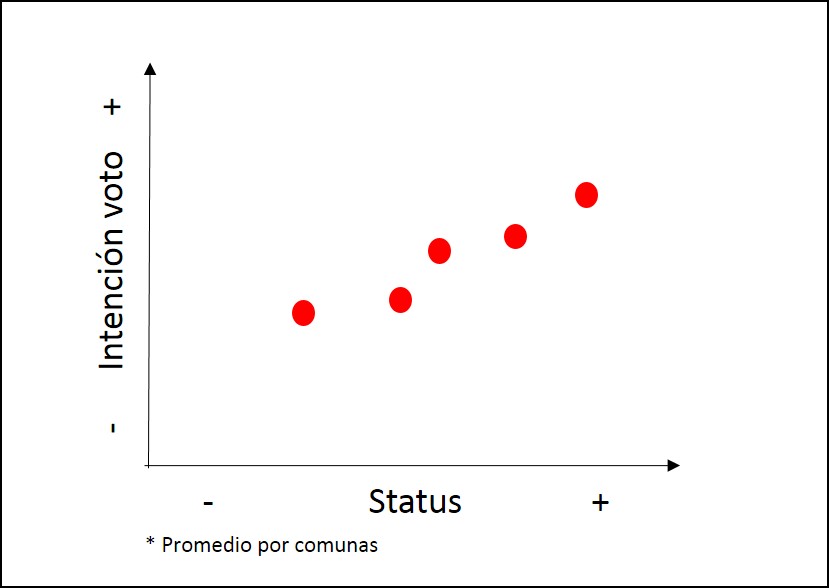
Falacia ecológica
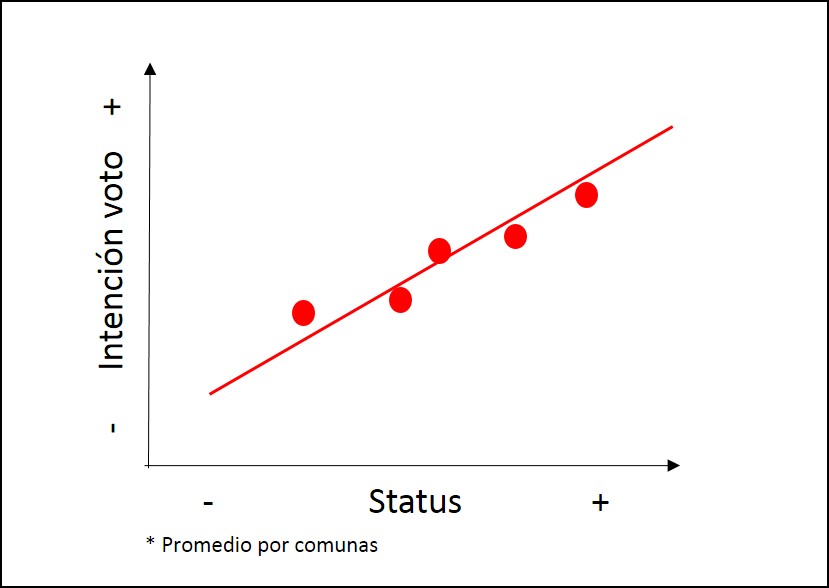
Falacia ecológica
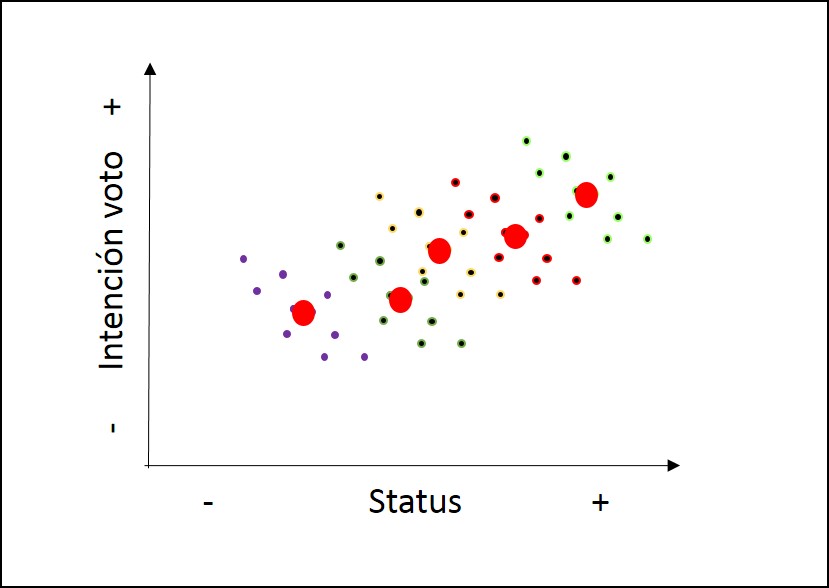
Falacia ecológica
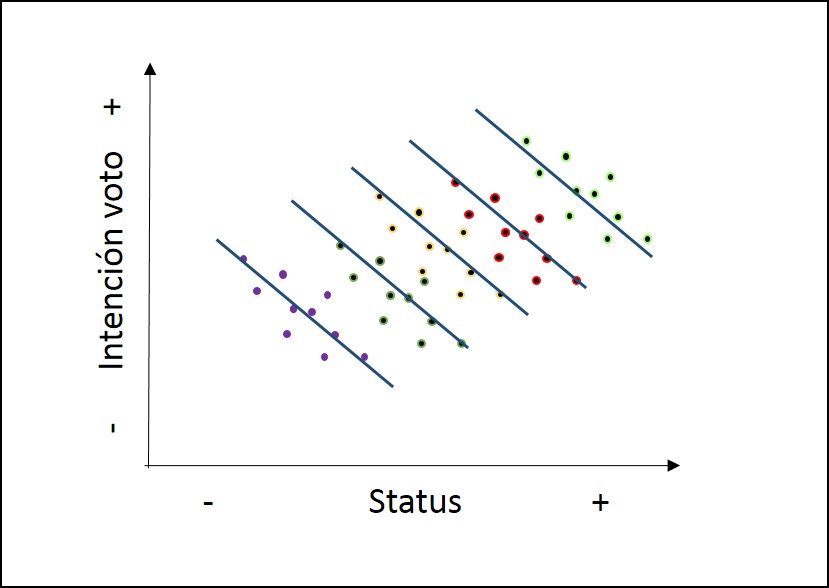
Falacia ecológica
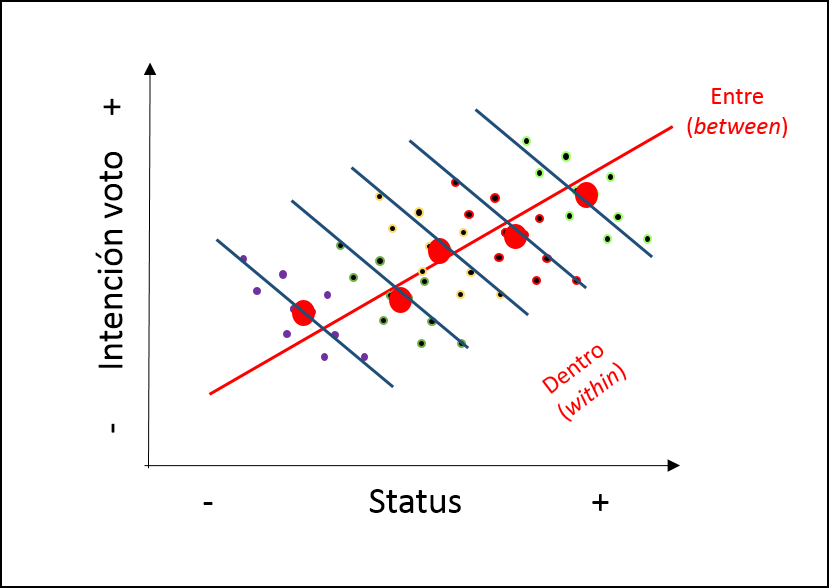
Implicancias falacia ecológica
- Relaciones individuales y contextuales no necesariamente van en la misma dirección (lineal)
Implicancias falacia ecológica
Relaciones individuales y contextuales no necesariamente van en la misma dirección (lineal)
Falacias también pueden ocurrir en la otra dirección (falacia individualista)
Implicancias falacia ecológica
Relaciones individuales y contextuales no necesariamente van en la misma dirección (lineal)
Falacias también pueden ocurrir en la otra dirección (falacia individualista)
Por lo tanto la inferencia ecológica (contextual) no se corresponde necesariamente con la inferencia individual
Implicancias falacia ecológica
Relaciones individuales y contextuales no necesariamente van en la misma dirección (lineal)
Falacias también pueden ocurrir en la otra dirección (falacia individualista)
Por lo tanto la inferencia ecológica (contextual) no se corresponde necesariamente con la inferencia individual
Distinguir ambos niveles es clave para estimación multinivel
Referencias
Blakely, T. A., & Woodward, A. J. (2000). Ecological effects in multi-level studies. Journal of Epidemiology and Community Health, 54(5), 367–374.
Robinson W S 1950. Ecological correlations and the behavior of individuals. American Sociological Review 15: 351–57
Contexto e implicancias teóricas
En el planteamiento de una investigación con hipótesis multinivel, es relevante definir:
Qué es el contexto
Cuáles son los elementos principales del contexto a considerar en las hipótesis
Cómo se relacionan variables del contexto con variables individuales (hipótesis)
Contexto e implicancias estadísticas
Los modelos multinivel tienen dos sentidos principales a nivel estadístico:
Corregir estimaciones con variables individuales cuando existe dependencia contextual (disminuye el error)
Hacen posible contrastar hipótesis que abarcan relaciones entre niveles, e incluir el contexto en el modelamiento estadístico
Modelos multinivel
Modelos multinivel
Definición minimalista: modelos de regresión que incluyen variables individuales y contextuales
Otras versiones/denominaciones:
- modelos jerárquicos
- modelos mixtos
- modelos contextuales
- modelos con efectos aleatorios
Tipos generales de problemas multinivel
Tres tipos de preguntas básicas, ejemplo educación:
¿Existen diferencias de rendimiento académico de los alumnos entre escuelas?
¿Tienen estas diferencias relación con variables de la escuela?
Las características de los estudiantes, ¿poseen un efecto distinto en rendimiento de acuerdo a características de las escuelas?
Formas de estimación multinivel
Base: modelo de regresión simple (no multinivel)
Formas de estimación multinivel
Predictor(es) individual(es) - (asumiendo contexto)
Formas de estimación multinivel
Predictor(es) contextual(es)

Formas de estimación multinivel
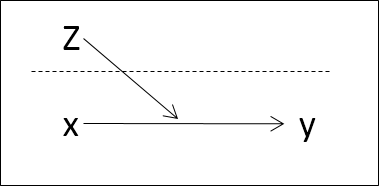
Modelo multinivel con predictores individuales y contextuales
Formas de estimación multinivel
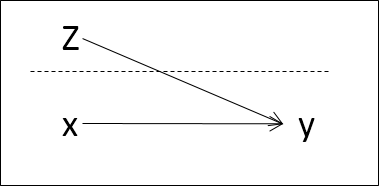
Modelo multinivel con interacción entre niveles
De la Práctica 2: Datos y estimación en 2 niveles
concepto de datos individuales y datos agregados
regresión en cada nivel de manera independiente
High School & Beyond (HSB) es una muestra representativa nacional de educación secundaria publica y católica de USA implementada por el National Center for Education Statistics (NCES).
Más información en https://nces.ed.gov/surveys/hsb/
Level 1 variables:
- minority, etnicidad (1 = minority, 0 =other)
- female, student gender (1 = female, 0 = male)
- ses, (medida estandarizada de nivel socioeconómico en base a variables como educación de los padres, ocupación e ingreso)
- mathach, logro en matemática (math achievement)
Práctica: High School & Beyond (HSB) data
Level 2 variables:
size (matricula)
sector (1 = Catholic, 0 = public)
pracad (proportion of students in the academic track)
disclim (a scale measuring disciplinary climate)
himnty (1 = more than 40% minority enrollment, 0 = less than 40%)
meanses (mean of the SES values for the students in this school who are included in the level-1 file)
Cluster variable= id (school id)
Librerías y datos
pacman::p_load(haven, # lectura de datos formato externocar, # varias funciones, ej scatterplotdplyr, # varios gestión de datosstargazer, # tablascorrplot, # correlacionesggplot2, # gráficoslme4) # multilevelmlm <-read_dta("http://www.stata-press.com/data/mlmus3/hsb.dta") # datosAjuste datos
dim(mlm)## [1] 7185 26names(mlm)## [1] "minority" "female" "ses" "mathach" "size" "sector" "pracad" ## [8] "disclim" "himinty" "schoolid" "mean" "sd" "sdalt" "junk" ## [15] "sdalt2" "num" "se" "sealt" "sealt2" "t2" "t2alt" ## [22] "pickone" "mmses" "mnses" "xb" "resid"Seleccionar variables de interés
mlm=mlm %>% select( minority,female,ses,mathach, # nivel 1 size, sector,mnses,schoolid) %>% # nivel 2 as.data.frame()Nota: sobre %>%
%>%es conocido como "pipe operator", operador pipa o simplemente pipaproviene de la librería
magrittr, que es utilizada endplyrobjetivo: hacer más fácil y eficiente el código, incorporando varias funciones en una sola línea / comando
avanza desde lo más general a lo más específico
Descriptivos generales
stargazer( as.data.frame(mlm), title = "Descriptivos generales", type='text')## ## Descriptivos generales## =================================================## Statistic N Mean St. Dev. Min Max ## -------------------------------------------------## minority 7,185 0.275 0.446 0 1 ## female 7,185 0.528 0.499 0 1 ## ses 7,185 0.0001 0.779 -3.758 2.692 ## mathach 7,185 12.748 6.878 -2.832 24.993## size 7,185 1,056.862 604.172 100 2,713 ## sector 7,185 0.493 0.500 0 1 ## mnses 7,185 0.0001 0.414 -1.194 0.825 ## schoolid 7,185 5,277.898 2,499.578 1,224 9,586 ## -------------------------------------------------Descriptivos generales
hist(mlm$mathach, xlim = c(0,30))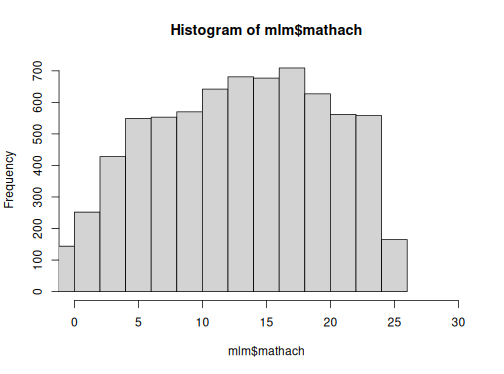
Descriptivos generales
scatterplot(mlm$mathach ~ mlm$ses, data=mlm, xlab="SES", ylab="Math Score", main="Math on SES", smooth=FALSE)
Descriptivos generales
cormat=mlm %>% select(mathach,ses,sector,size, mnses) %>% cor()round(cormat, digits=2)## mathach ses sector size mnses## mathach 1.00 0.36 0.20 -0.05 0.34## ses 0.36 1.00 0.19 -0.07 0.53## sector 0.20 0.19 1.00 -0.42 0.36## size -0.05 -0.07 -0.42 1.00 -0.13## mnses 0.34 0.53 0.36 -0.13 1.00Descriptivos generales
corrplot.mixed(cormat)
Datos agregados
Se procede a "agregar", generando una base de datos a nivel 2
Usando la funcion
group_by(agrupar por) de la libreríadplyrSe agrupa por la variable cluster, que identifica a las unidades de nivel 2 (en este caso,
schoolid)- Por defecto se hace con el promedio, pero se pueden hacer otras funciones como contar, porcentajes, mediana, etc.
Generando base de datos agregados
agg_mlm=mlm %>% group_by(schoolid) %>% summarise_all(funs(mean)) %>% as.data.frame()generamos el objeto
agg_mlmdesde el objetomlmagrupando por la variable cluster
schoolidagregamos (colapsamos) todas
summarise_allpor el promediofuns(mean)
Datos agregados
stargazer(agg_mlm, type = "text")## ## ===============================================## Statistic N Mean St. Dev. Min Max ## -----------------------------------------------## schoolid 160 5,309.994 2,547.683 1,224 9,586 ## minority 160 0.275 0.301 0.000 1.000 ## female 160 0.519 0.256 0.000 1.000 ## ses 160 -0.006 0.414 -1.194 0.825 ## mathach 160 12.621 3.118 4.240 19.719## size 160 1,097.825 629.506 100 2,713 ## sector 160 0.438 0.498 0 1 ## mnses 160 -0.006 0.414 -1.194 0.825 ## -----------------------------------------------Comparación Modelos
- Modelo con datos individuales
reg<- lm(mathach~ses+female+sector, data=mlm)- Modelo con datos agregados
reg_agg<- lm(mathach~ses+female+sector, data=agg_mlm)- Generación tabla
stargazer(reg,reg_agg, column.labels=c("Individual","Agregado"), type ='text')Comparación Modelos
pacman::p_load(sjPlot,sjmisc,sjlabelled)tab_model(reg, reg_agg, show.ci=F, show.se = T, dv.labels = c("Individual", "Agregado"))| Individual | Agregado | |||||
|---|---|---|---|---|---|---|
| Predictors | Estimates | std. Error | p | Estimates | std. Error | p |
| (Intercept) | 12.52 | 0.13 | <0.001 | 13.13 | 0.35 | <0.001 |
| ses | 2.88 | 0.10 | <0.001 | 5.19 | 0.37 | <0.001 |
| female | -1.40 | 0.15 | <0.001 | -1.97 | 0.56 | 0.001 |
| sector | 1.96 | 0.15 | <0.001 | 1.25 | 0.31 | <0.001 |
| Observations | 7185 | 160 | ||||
| R2 / R2 adjusted | 0.160 / 0.159 | 0.675 / 0.668 | ||||
¿Qué problema puede haber al estimar un mismo modelo para variables individuales y agregadas?
Regresión con más de 1 nivel
Residuos y dependencia contextual
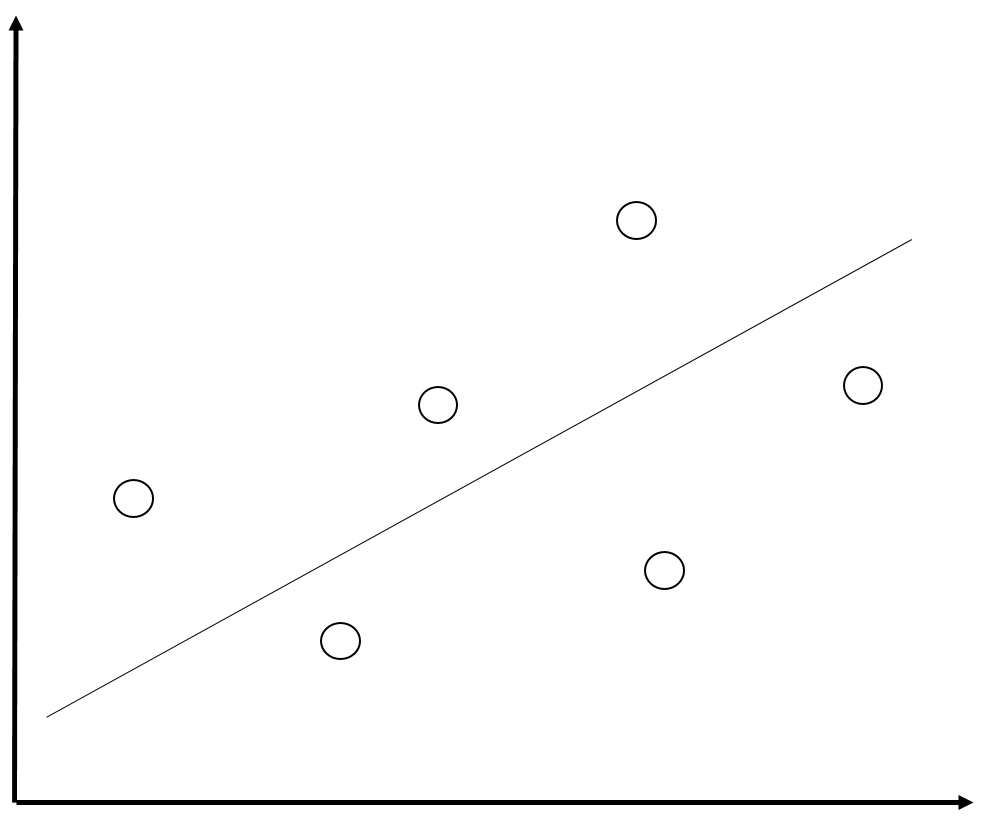
Residuos y dependencia contextual
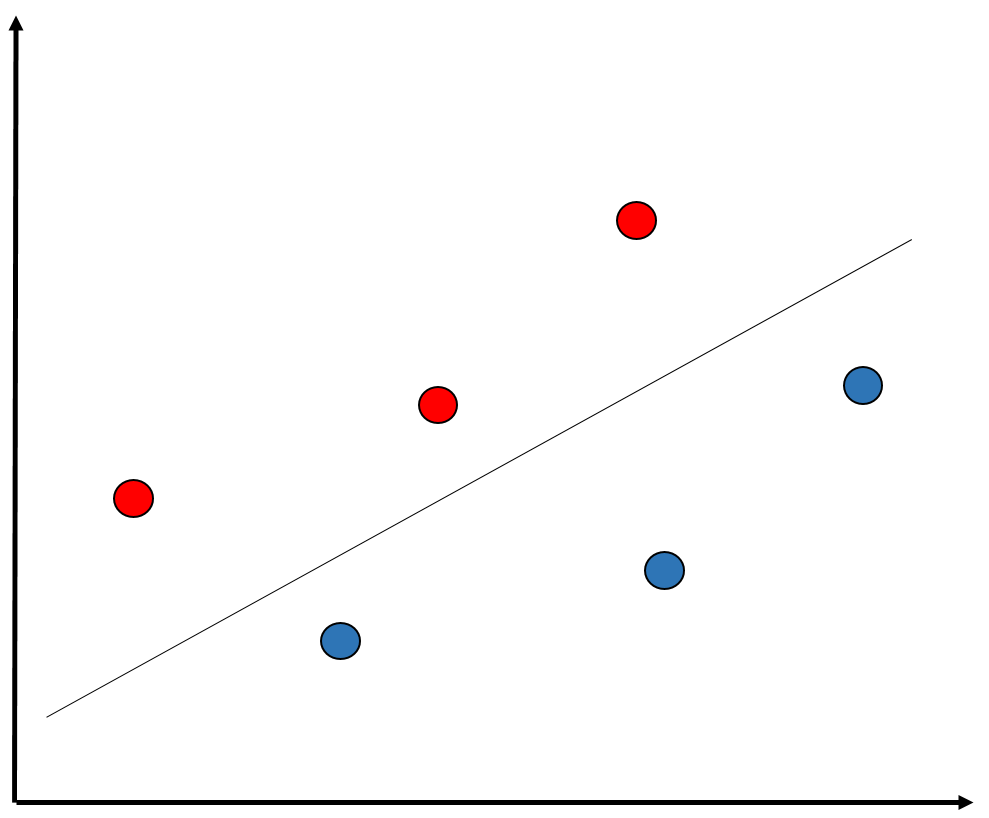
Residuos y dependencia contextual
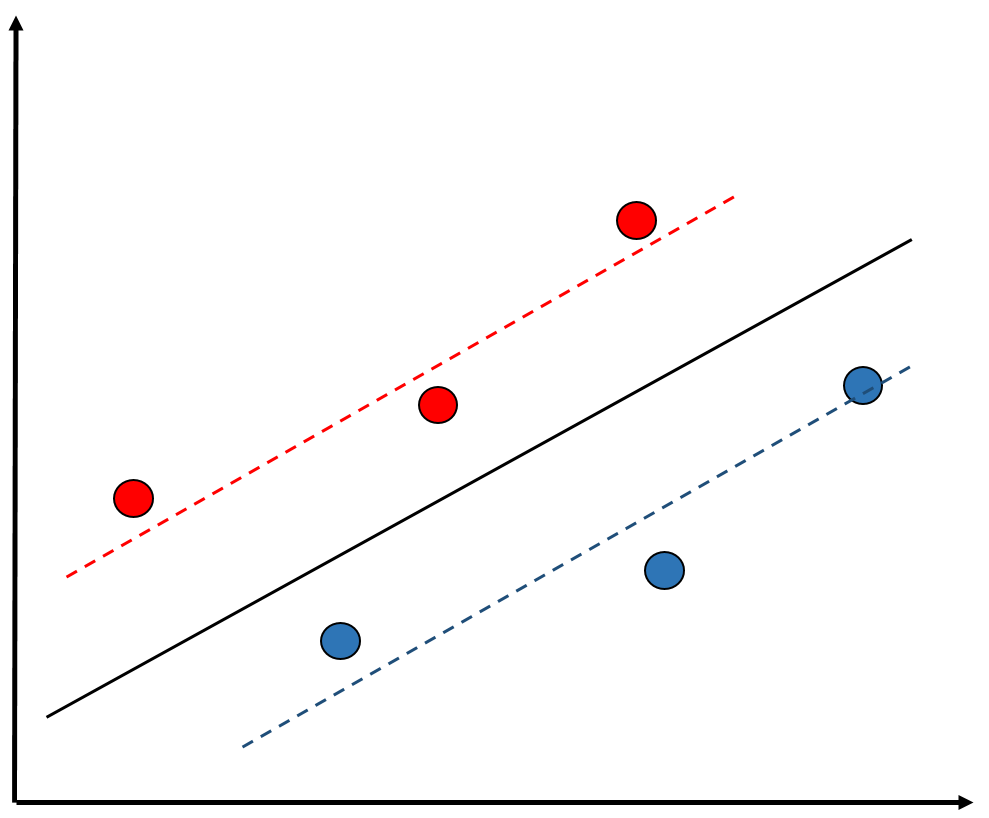
Residuos y dependencia contextual
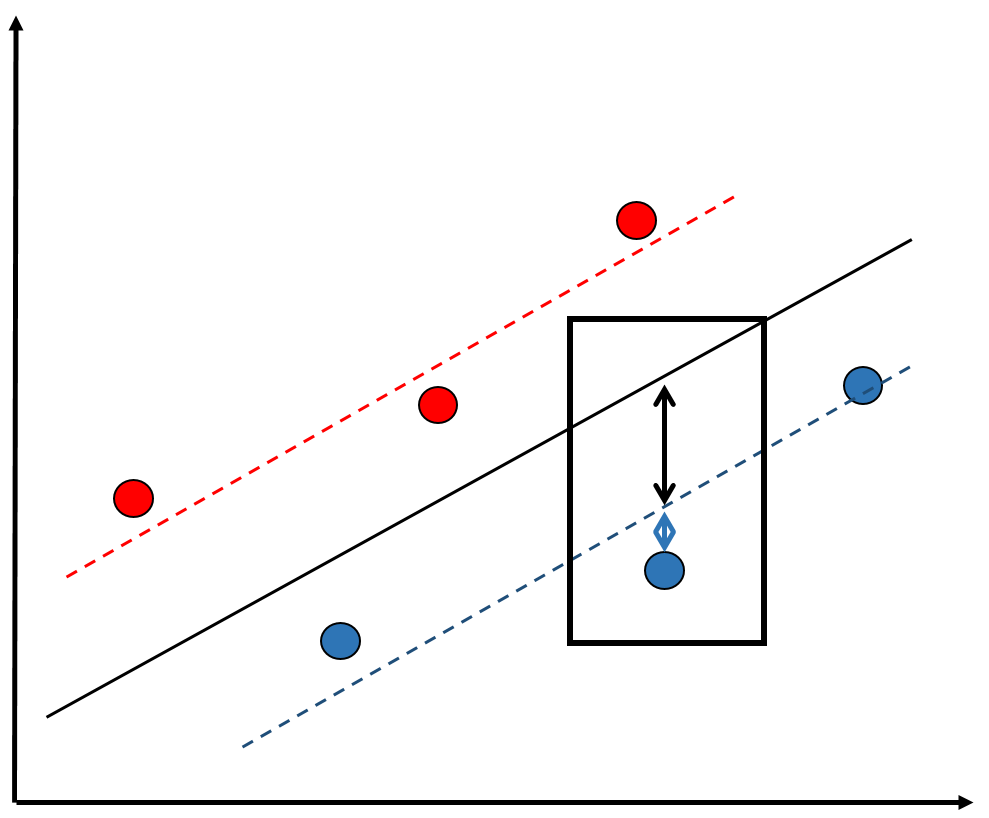
Implicancias para el modelo de regresión:
Situaciones en que los residuos son distintos de manera sistemática de acuerdo a variables contextuales: dependencia (contextual) de los residuos
Si un modelo de regresión de 1 nivel se aplica en situaciones de dependiencia contextual, entonces puede aumentar el error en la estimación
Alternativas
Descomposición de la varianza de los residuos entre y dentro los grupos= en distintos niveles = multinivel.
En concreto, se agrega un término de error adicional al modelo: μ0j
Este término de error se expresa como un efecto aleatorio (como opuesto a efecto fijo)
Regresión a distintos niveles
Modelo con coeficientes aleatorios (RCM)
Random Coefficients Models (RCM) o Mixed (effects) Models
Forma de estimación de modelos multinivel
Idea base: se agrega un parámetro aleatorio al modelo, es decir, que posee variación en relación a unidades de nivel 2.
Modelos multinivel
