Modelos multinivel

Unidades en contexto
Sesión 6:
Ajuste y Reporte
Lecturas
- O’Conell & McCoach 7, Evaluating model fit and adequacy
- O’Conell & McCoach 11, Reporting results from multilevel
Contenidos
1- Resumen sesión anterior
2- Ajuste
3- Reporte
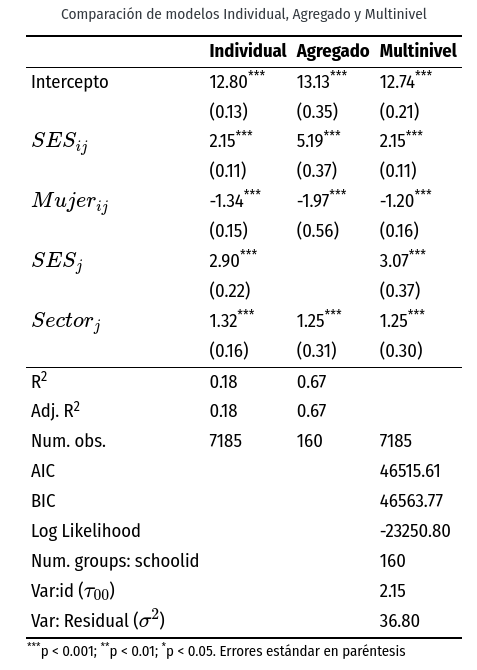
Comparación Modelos
- Modelo con datos individuales
reg<- lm(mathach~ses+female+sector, data=mlm)- Modelo con datos agregados
reg_agg<- lm(mathach~ses+female+sector, data=agg_mlm)Comparación Modelos
pacman::p_load(sjPlot,sjmisc,sjlabelled)tab_model(reg, reg_agg, show.ci=F, show.se = T, dv.labels = c("Individual", "Agregado"))| Individual | Agregado | |||||
|---|---|---|---|---|---|---|
| Predictors | Estimates | std. Error | p | Estimates | std. Error | p |
| (Intercept) | 12.52 | 0.13 | <0.001 | 13.13 | 0.35 | <0.001 |
| ses | 2.88 | 0.10 | <0.001 | 5.19 | 0.37 | <0.001 |
| female | -1.40 | 0.15 | <0.001 | -1.97 | 0.56 | 0.001 |
| sector | 1.96 | 0.15 | <0.001 | 1.25 | 0.31 | <0.001 |
| Observations | 7185 | 160 | ||||
| R2 / R2 adjusted | 0.160 / 0.159 | 0.675 / 0.668 | ||||
Implicancias estimación individual/agregada
- inflación de errores estándar para variables nivel 1 estimadas como agregadas, ej: female agregado (riesgo error tipo II) -> no detectar un efecto cuando este existe
Implicancias estimación individual/agregada
- inflación de errores estándar para variables nivel 1 estimadas como agregadas, ej: female agregado (riesgo error tipo II) -> no detectar un efecto cuando este existe
- contracción de errores estándar para variables nivel 2 estimadas como individuales, ej: sector individual (error tipo I) -> detectar un efecto cuando este no existe
Componentes de la varianza
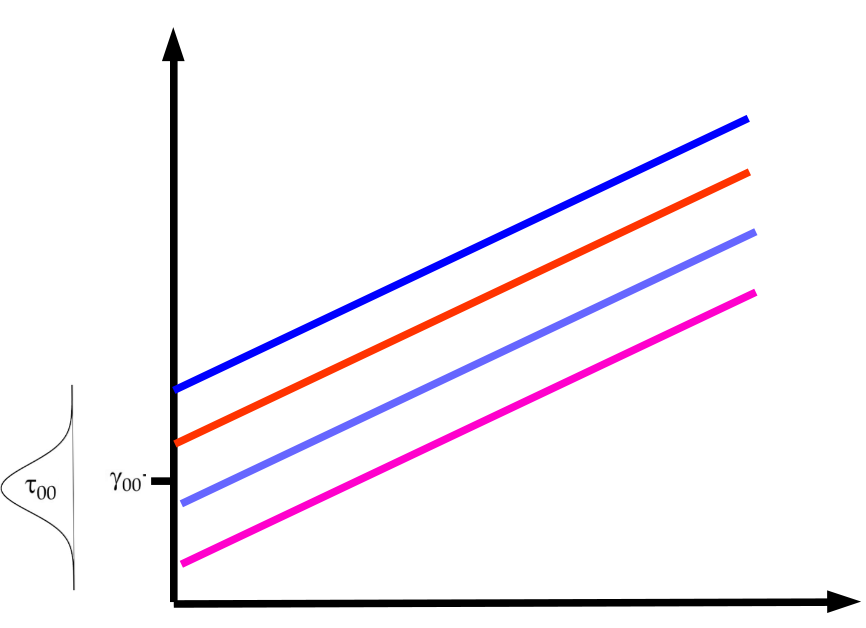
Componentes de la varianza
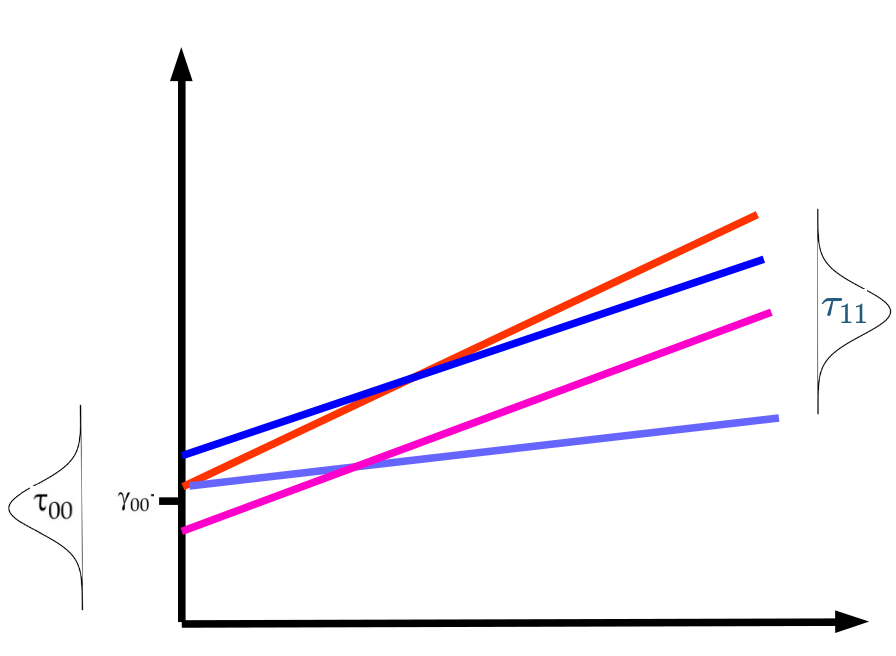
Correlación intra clase: ICC
- La correlación intra-clase ( ρ ) indica qué porcentaje de la varianza de la variable dependiente se debe a pertenencia a unidades de nivel 2
Correlación intra clase: ICC
- La correlación intra-clase ( ρ ) indica qué porcentaje de la varianza de la variable dependiente se debe a pertenencia a unidades de nivel 2
- Descomposición de la varianza en modelo nulo= Var y=τ00+σ2
Correlación intra clase: ICC
- La correlación intra-clase ( ρ ) indica qué porcentaje de la varianza de la variable dependiente se debe a pertenencia a unidades de nivel 2
- Descomposición de la varianza en modelo nulo= Var y=τ00+σ2
- Es decir, parte de la varianza se debe a los individuos ( σ2 ) y parte al grupo ( τ00 )
Correlación intra clase: ICC
- Correlación intra-clase = ICC =
ρ=τ00τ00+σ2
- Una ICC baja indica baja variabilidad de la variable dependiente entre unidades de nivel 2, y por lo tanto, menores posibilidades de dar cuenta (explicar) de esa varianza con predictores de nivel 2.
Correlación intra-clase
"Proporción de la varianza de la variable dependiente que se asocia a la pertenencia a unidades de nivel 2"
librería lme4
función lmer (linear mixed effects)
forma general:
objeto <- lmer (depvar ~ predictor_1 + predictor_2 + predictor_n + (1 | cluster), data=data)el objeto contiene la información de la estimación; para ver un resumen,
summary(objeto), y de manera más presentable,screenreg(objeto)
Contenidos
1- Resumen sesión anterior
2- Ajuste
3- Reporte
Tipos de medidas de ajuste
Medidas relativas a la varianza de efectos aleatorios (tipo R2)
Medidas de fit comparativo (deviance)
Ajuste por proporción de varianzas

Estimación de modelos para el ejemplo:
results_0: nulo results_1: agrega predictores individuales (nivel 1) results_2: agrega predictores grupales (nivel 2)
results_0 <-lmer(mathach ~ 1 + (1 | schoolid), data = mlm)results_1 <-lmer(mathach ~ 1 + ses + female + (1 | schoolid), data = mlm)results_2 <-lmer(mathach ~ 1 + sector + mnses + (1 | schoolid), data = mlm)Ajuste por proporción de varianzas
Se relacionan con el grado de varianza “explicada” (disminución en la(s) varianza(s) atribuida a la inclusión de predictores en el modelo de regresión)
Controversia en la literatura de multinivel, no existe una medida única
Las propuestas sugieren usualmente cálculos de R2 para cada nivel
Bryck & Raudenbush R2 multinivel (1992)
- lógica general: calcular la diferencia entre componentes de la varianza entre los modelos estimados
Bryck & Raudenbush R2 multinivel (1992)
lógica general: calcular la diferencia entre componentes de la varianza entre los modelos estimados
modelo base para la comparación: modelo nulo
Bryck & Raudenbush R2 multinivel (1992)
lógica general: calcular la diferencia entre componentes de la varianza entre los modelos estimados
modelo base para la comparación: modelo nulo
luego, al ir estimando nuevos models con más predictores, se compara (con el modelo nulo) en que medida los componentes de la varianza van disminuyendo
Componentes de la varianza del ejemplo modelos con HSB data
| σ2 | τ00 | |
|---|---|---|
| Modelo 0 (nulo, sin predictores) | 39.148 | 8.553 |
| Modelo 1 (predictores ind.) | 36.813 | 4.492 |
| Modelo 2 (predictores grup.) | 39.161 | 2.314 |
Los componentes de la varianza van disminuyendo a medida que se ingresan predictores a los modelos
Por ejemplo, en el modelo 1 el componente de la varianza individual σ2 disminuye en comparación al modelo nulo: 39.148-36.813=2.335 - ¿Cómo interpretar esto?
Bryk & Raudenbush - R2 Nivel 1
Para Nivel 1:
R21B&R=var0(rij)−varf(rij)var0(rij)=σ2(0)−σ2(f)σ2(0)
Donde:
0 se refiere al modelo nulo
f se refiere a un modelo posterior
Bryk & Raudenbush - R2 Nivel 1
| σ2 | τ00 | R2L1 | R2L2 | |
|---|---|---|---|---|
| Modelo 0 | 39.148 | 8.553 | ||
| Modelo 1 (predict.ind.) | 36.813 | 4.492 | 0.059 | |
| Modelo 2 (predict.grup.) | 39.161 | 2.314 |
Ej: R2L1=(39.148−36.813)/39.148=2.335/39.148=0.059
Bryck & Raudenbush - R2 Nivel 2
Para Nivel 2:
R22B&R=var0(μ0j)−varf(μ0j)var0(μ0j)=τ00(0)−τ00(f)τ00(0)
Donde:
0 se refiere al modelo nulo
f se refiere a un modelo posterior
Bryck & Raudenbush - R2 Nivel 2
| σ2 | τ00 | R2L1 | R2L2 | |
|---|---|---|---|---|
| Modelo 0 | 39.148 | 8.553 | ||
| Modelo 1 (predict.ind.) | 36.813 | 4.492 | 0.059 | |
| Modelo 2 (predict.grup.) | 39.161 | 2.314 | 0.00 | 0.73 |
Ej: R2L2=(8.553−2.314)/8.553=6.239/8.553=0.73
Bryck & Raudenbush - R2 Nivel 2
| σ2 | τ00 | R2L1 | R2L2 | |
|---|---|---|---|---|
| Modelo 0 | 39.148 | 8.553 | ||
| Modelo 1 (predict.ind.) | 36.813 | 4.492 | 0.059 | |
| Modelo 2 (predict.grup.) | 39.161 | 2.314 | 0.00 | 0.73 |
Ej: R2L2=(8.553−2.314)/8.553=6.239/8.553=0.73
- Recordar interpretación en relación a correlación intra-clase (para el caso de HSB data= 0.18): para el caso del R2 nivel 2 se está dando cuenta del 73% del 18%
Cálculo directo con R - modelo 1
función multilevel.r2, librería misty
pacman::p_load(misty)# for multilevel R2misty::multilevel.r2(results_1, print = "RB")## R-Squared Measures for Multilevel and Linear Mixed Effects Models## ## Reduction in Residual Variance (Raudenbush and Bryk, 2002)## ## Within-Cluster R2: 0.060 ## Between-Cluster R2: 0.479Cálculo directo Bryk & Raudenbush con R - modelo 2
función multilevel.r2, librería misty
pacman::p_load(misty)# for multilevel R2misty::multilevel.r2(results_2, print = "RB")## R-Squared Measures for Multilevel and Linear Mixed Effects Models## ## Reduction in Residual Variance (Raudenbush and Bryk, 2002)## ## Within-Cluster R2: -0.000 ## Between-Cluster R2: 0.731Nakagawa and Schielzeth R2 (2013)
dos R2:
marginal: para los efectos fijos del modelo
condicional: para el modelo con efectos fijos y aleatorios
utiliza la varianza de los valores predichos de la variable dependiente
Nakagawa and Schielzeth R2 (2013)
- marginal (efectos fijos): R2m=var(^Yij)var(^Yij)+τ00+σ2
- condicional (efectos fijos + aleatorios) R2c=var(^Yij)+τ00var(^Yij)+τ00+σ2
Cálculo directo Nakagawa con R - modelo 2
misty::multilevel.r2(results_2, print = "NS")## R-Squared Measures for Multilevel and Linear Mixed Effects Models## ## Variance Partitioning (Nakagawa and Schielzeth, 2013; Johnson, 2014)## ## Marginal R2: 0.130 ## Conditional R2: 0.1792. Ajuste comparativo
Deviance test
El test o estadístico de deviance compara el ajuste de dos modelos basado en la log verosimilitud de cada modelo
La hipótesis a contrastar es si predictores adicionales del modelo mejoran o no el ajuste
Asume que los modelos son anidados, es decir, que un modelo con menos predictores puede ser derivado del modelo mayor mediante la fijación de ciertos coeficientes como 0.
Deviance= −2∗LL (LL=Log Likelihood)
Deviance test= deviance(anidado)−deviance(mayor)
2. Ajuste comparativo
Deviance test
La distribución del estadístico de devianza es χ2, y los grados de libertad para calcular el valor crítico equivalen al número de parámetros extra en el modelo mayor
Es decir, parámetros modelo mayor - parámetros modelo inicial (o anterior)
Se utiliza con estimación ML en lugar de REML (restricted maximum likelihood).
Ejemplo deviance
results_0ml = lmer(mathach ~ 1 + (1 | schoolid), REML=FALSE)results_1ml = lmer(mathach ~ 1 + minority + ses + (1 | schoolid), REML=FALSE)| LL | deviance | Parámetros | |
|---|---|---|---|
| results_0ml | -23557.91 | 47115.81 | |
| results_1ml | -23221.82 | 46443.64 | 2 |
- Deviance test= 47115.8-46443.64= 672.16, 2 DF (2 parámetros adicionales)
Ejemplo deviance
Valor crítico χ2DF=2 para p<0.95=5.99
Por lo tanto, se rechaza H0, es decir, las diferencias entre los modelos son distintas de 0 ( p<0.05 ). En otras palabras, el modelo con más parámetros presenta un mejor ajuste.
Ejemplo deviance II - de manera directa en R:
anova(results_0ml,results_1ml)Y para reportar:
print(xtable::xtable(anova(results_0ml,results_1ml)), type="html")
| npar | AIC | BIC | logLik | deviance | Chisq | Df | Pr(>Chisq) | |
|---|---|---|---|---|---|---|---|---|
| results_0ml | 3.00 | 47121.81 | 47142.45 | -23557.91 | 47115.81 | |||
| results_1ml | 5.00 | 46453.64 | 46488.03 | -23221.82 | 46443.64 | 672.17 | 2 | 0.0000 |
Ajuste y modelos con pendiente aleatoria
Los test de ajuste por proporción de varianza (R2) no son recomendados al momento de estimar modelos con pendiente aleatoria
El test de deviance se utiliza al momento de reportar la significancia de los efectos aleatorios (ej: con pendiente aleatorio,comparando el mismo modelo con y sin aleatorización)
Considerar que los componentes de la varianza son parámetros del modelo, es decir, se cuentan para la diferencia de grados de libertad
Contenidos
1- Resumen sesión anterior
2- Ajuste
3- Reporte
Tablas y descriptivos
Tabla de descriptivos de variables L1 y L2
para esto conviene generar base de datos agregados para tabla descriptiva
se recomienda utilizar librería summarytools, función dfSummary (información aquí)
Descripción del número de casos por nivel y también de otras variables relevantes (ej, dependiente e independientes comprometidas en hipótesis)
sjmisc::descr(mlm, show = c("label","range", "mean", "sd", "NA.prc", "n"))%>% kable(.,digits =2,"markdown")| var | label | n | NA.prc | mean | sd | range | |
|---|---|---|---|---|---|---|---|
| 3 | minority | minority | 7185 | 0 | 0.27 | 0.45 | 1 (0-1) |
| 1 | female | female | 7185 | 0 | 0.53 | 0.50 | 1 (0-1) |
| 7 | ses | ses | 7185 | 0 | 0.00 | 0.78 | 6.45 (-3.76-2.69) |
| 2 | mathach | mathach | 7185 | 0 | 12.75 | 6.88 | 27.83 (-2.83-24.99) |
| 8 | size | size | 7185 | 0 | 1056.86 | 604.17 | 2613 (100-2713) |
| 6 | sector | sector | 7185 | 0 | 0.49 | 0.50 | 1 (0-1) |
| 4 | mnses | mnses | 7185 | 0 | 0.00 | 0.41 | 2.02 (-1.19-0.82) |
| 5 | schoolid | schoolid | 7185 | 0 | 5277.90 | 2499.58 | 8362 (1224-9586) |
Problema tabla anterior: aparecen en conjunto variables de nivel 1 y nivel 2, tienen distinto N y deberían presentarse por separado
mlm %>% select (mathach, ses, female, minority) %>% sjmisc::descr(., show = c("label","range", "mean", "sd", "NA.prc", "n"))%>% kable(., digits =2, "markdown", caption = "Variables nivel 1")Table: Variables nivel 1
| var | label | n | NA.prc | mean | sd | range | |
|---|---|---|---|---|---|---|---|
| 2 | mathach | mathach | 7185 | 0 | 12.75 | 6.88 | 27.83 (-2.83-24.99) |
| 4 | ses | ses | 7185 | 0 | 0.00 | 0.78 | 6.45 (-3.76-2.69) |
| 1 | female | female | 7185 | 0 | 0.53 | 0.50 | 1 (0-1) |
| 3 | minority | minority | 7185 | 0 | 0.27 | 0.45 | 1 (0-1) |
agg_mlm %>% select (size, sector,mnses) %>% sjmisc::descr(., show = c("label","range", "mean", "sd", "NA.prc", "n"))%>% kable(., digits =2, "markdown", caption = "Variables nivel 2")Table: Variables nivel 2
| var | label | n | NA.prc | mean | sd | range | |
|---|---|---|---|---|---|---|---|
| 3 | size | size | 160 | 0 | 1097.83 | 629.51 | 2613 (100-2713) |
| 2 | sector | sector | 160 | 0 | 0.44 | 0.50 | 1 (0-1) |
| 1 | mnses | mnses | 160 | 0 | -0.01 | 0.41 | 2.02 (-1.19-0.82) |
Descriptivos
Ejemplo tabla descriptiva (Ferron et al 2007, en O’Connell Cap.11)
Alternativas en R: Stargazer, summarytools
Reporte modelos
(O’Connell, cap.11)
Reporte modelos
Reporte modelos
Efectos fijos, con valores t o se
Asteriscos para niveles de significación
Efectos aleatorios
Fit: log likelihood
Fit adicionales: AIC, BIC, deviance, R2
Reporte con tab_model
tab_model(results_1, results_2, show.ci = FALSE, show.se = TRUE, collapse.se = TRUE, show.p = FALSE, p.style = c("scientific_stars") )| mathach | |
|---|---|
| Predictors | Estimates |
| (Intercept) | 12.13 *** (0.20) |
| sector | 1.23 *** (0.31) |
| mnses | 5.33 *** (0.37) |
| Random Effects | |
| σ2 | 39.16 |
| τ00 schoolid | 2.31 |
| ICC | 0.06 |
| N schoolid | 160 |
| Observations | 7185 |
| Marginal R2 / Conditional R2 | 0.130 / 0.179 |
| * p<0.05 ** p<0.01 *** p<0.001 | |
Reportes de relaciones bivariadas
- tablas cruzadas
- correlaciones / corrplot
- nubes de puntos
Revisar:
Sobre reporte reproducible
Ventajas
permite generar tablas y gráficos automáticamente en el mismo documento, evitando el cortar / pegar
escritura simple
Desventajas
acostumbrarse
conformarse con un formato simple de texto (al menos inicialmente)
... igual es R
VALE LA PENA
RMarkdown / Quarto
Tres cosas básicas a aprender:
Markdown
Insertar trozos (chunks) de código
Opciones generales en encabezado YAML
Varios tutoriales ... revisar
Guías de documentos dinámicos (con video) de clases de correlacional 2023:
Modelos multinivel