Modelos multinivel

Unidades en contexto
Sesión 8:
Centrado
Bases: Centrado en regresión simple
¿Qué es el centrado?
- es un ajuste en la escala de los predictores en torno a un valor central (usualmente el promedio)
¿Para qué?
- porque el valor de los predictores (en su escala original) tiene consecuencias para la predicción que se puede hacer desde un modelo de regresión
Ejemplo centrado
> mydata ci mean_ci cicent_mean 1 90 97 -7 2 95 97 -2 3 98 97 1 4 105 97 8 Ejemplo centrado
> mydata ci mean_ci cicent_mean 1 90 97 -7 2 95 97 -2 3 98 97 1 4 105 97 8 cicent_meanes la variablecicentrada al promedio
Regresión y centrado
- El centrado de las variables en regresión OLS posee consecuencias en el valor del intercepto
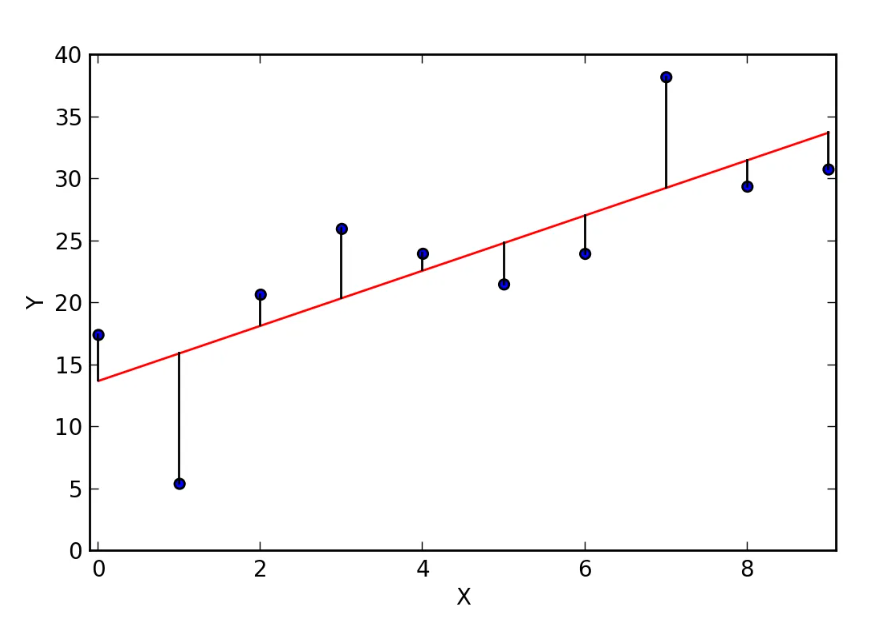
Regresión y centrado
- El centrado de las variables en regresión OLS posee consecuencias en el valor del intercepto

- Intercepto: estimación del valor de la variable dependiente cuando el/los predictor/es son
0
Regresión y centrado (2)
usualmente los predictores se utilizan en su escala original (sin centrar)
La estimación sin centrar en algunos casos puede llevar a algunos problemas en la interpretación de los parámetros del modelo
El centrado se implementa restando una constante del predictor (usualmente el promedio)
Ejemplo centrado regresión simple
Datos: puntaje en CI y en una escala de felicidad 1-7
> mydata felicidad ci1 1 902 3 953 4 984 6 105lm(formula = felicidad ~ ci)(Intercept) ci-28.5593 0.3305¿Qué significa el valor del intercepto?
Ejemplo (no) centrado en regresión simple
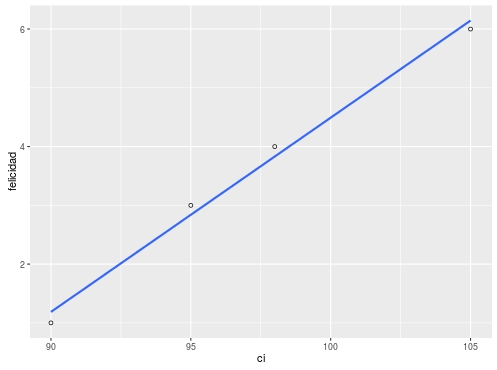
Ejemplo (no) centrado en regresión simple
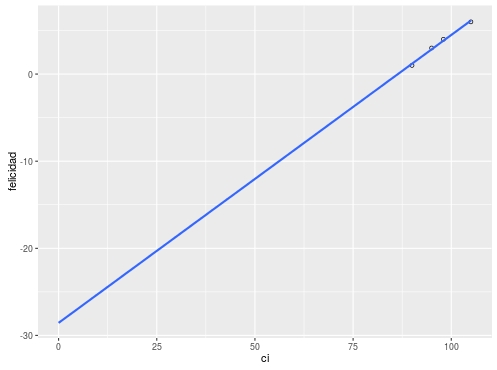
Ejemplo centrado regresión simple
> mydata felicidad ci mean_ci cicent_mean cicent_1001 1 90 97 -7 -102 3 95 97 -2 -53 4 98 97 1 -24 6 105 97 8 5lm(formula = felicidad ~ cicent_mean)(Intercept): 3.5000 ; cicent_mean:0.3305lm(formula = felicidad ~ cicent_100)(Intercept): 4.4915 ; mydata$cicent_100: 0.3305Ejemplo centrado en regresión simple - al promedio
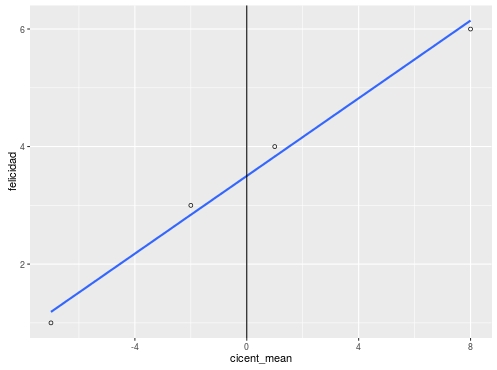
Ejemplo centrado en regresión simple -centrado en 100
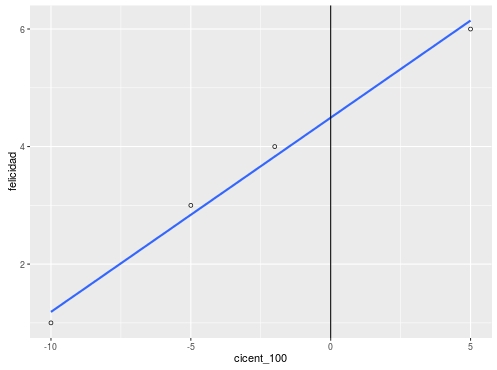
Ejemplo centrado regresión simple: RESUMEN
β constante en todos los modelos, varía solo intercepto
- modelo sin centrar: intercepto -28,5, felicidad para alguien con inteligencia 0 (no tiene mucho sentido ...)
centrado al promedio: 3.5, estimación de la felicidad para alguien con inteligencia promedio
centrado a 100: 4.49, estimación de la felicidad para alguien con inteligencia 100
Centrado en modelos multinivel
Texto clave:
Enders, C. K., & Tofighi, D. (2007). Centering predictor variables in cross-sectional multilevel models: A new look at an old issue. Psychological Methods, 12(2), 121–138.
(Acceso aquí)
Distintos centrados según nivel
- En MLM, las posibilidades de centrado se amplían según la cantidad de niveles que se tengan
Distintos centrados según nivel
En MLM, las posibilidades de centrado se amplían según la cantidad de niveles que se tengan
Tomando como referencia dos niveles, el centrado de los predictores de nivel uno puede tomar 2 formas principales:
a la gran media o promedio general (CGM - centered grand mean)
al promedio al interior (within) de grupos/clusters (CWC - centered within clusters)
(nomenclatura Enders & Tofighi, 2007)
Distintos centrados según nivel
El CGM (a la gran media) es equivalente al de regresión simple para el mismo propósito: se resta el valor del promedio general
En el CWC (a la media grupal) se resta el promedio del grupo (es decir, para cada grupo) en lugar de la gran media
Distintos centrados según nivel
A diferencia de regresión simple, las decisiones respecto de centrado afectan más allá del valor del intercepto, influyendo en:
valor de β
componentes de la varianza ( τ00,τ11,τ01)
interacciones entre niveles
CGM y CWC estiman la relación entre X e Y de distinta manera y producen intepretaciones distintas de los parámetros
Which form of centering provides interpretable parameter estimates that can be used to address a particular substantive research question?
(Enders & Tofighi 2007, p. 122)
Distintos centrados según nivel
Ejemplo: dataset artificial que maximiza las diferencias entre clusters para mostrar mejor los efectos de los distintos tipos de centrado (Enders & Tofighi, 2007)
Variable dependiente: bienestar
Variable independiente nivel 1 ( γ10 )= horas de trabajo
Variable independiente nivel 2 ( γ01 )= tamaño del grupo
Centrado a la gran media
CGM - centrado a la gran media
La relación entre las horas de trabajo y bienestar posee componentes a nivel 1 y nivel 2
Individuos que trabajan más tienen a tener menor bienestar (L1)
Grupos que en promedio trabajan menos poseen menores niveles de bienestar (L2)
Como en regresión simple, en CGM no se altera la estimación de β, solo varía la estimación del valor del intercepto ... además de alterar otros parámetros (detalles más adelante)
Centrado al grupo (1)
Comparación con centrado al grupo
A diferencia del centrado a la gran media (que altera el valor del intercepto), el centrado al grupo cambia la estructura de la variable, y afecta tanto al beta como al intercepto
Correlaciones entre especificaciones de centrado
La correlación entre variables no varia entre puntajes brutos y centrados CGM
El CWC crea una variable distinta, y por tanto correlaciona distinto con otras
La variable CGM correlaciona tanto con predictores de nivel 1 como de nivel 2 (contiene en su covariación una dimiension between)
La variable CWC correlaciona 0 con predictores de nivel 2 (porque su varianza a nivel 2 es 0)
En términos de regresión:
Regresión multinivel y centrado
OLS puede verse como una combinación ponderada de los coeficientes between y within clusters
En CGM, γ10 es una mezcla de asociación within y between:
- “the hierarchical estimator under grand-mean centering is an inappropriate estimator of the person-level [i.e., Level 1] effect. It too is an uninterpretable blend: neither βw nor βb” (Raudenbush and Bryk, 2002, p. 139).
Regresión multinivel y centrado
- En CGM, se altera también la estimación de la varianza de las pendientes ( τ11 ) al incorporar elementos between que pueden reducir variabilidad:
En CWC (1):
No contiene variación entre clusters y por lo tanto no correlaciona con variables de nivel 2
El intercepto se interpreta como el promedio no ajustado del promedio de los clusters
Por lo tanto, con predictores CWC, γ00 es equivalente al del modelo nulo
En CWC (2):
En CWC la pendiente corresponde a la regresión within cluster, es un estimador “puro” de la relación nivel 1 entre x e y
La estimación de τ00 con un predictor CWC cuantifica la varianza de los promedios no ajustados; por lo tanto debería ser similar a la de un modelo incondicional (sin predictores)
Centrado y 4 posibles focos de investigación
Predictor de nivel 1
Predictor de nivel 2
Comparar la influencia de un predictor a distintos niveles
Efectos de interacción
1. Predictor de nivel 1
Se recomienda CWC
Estimador “puro” de efectos nivel 1
Estimación más adecuada de la varianza de la pendiente
Sustantivamente: la posición relativa respecto del grupo es un determinante relevante para los individuos (comportamientos, actitudes, etc.)
2. Predictor de nivel 2
Si solo hay predictores de nivel 2, seguir recomendaciones de centrado de OLS
Cuando hay predictores de nivel 1, se recomienda CGM, ya que como contiene varianza between ajusta la estimación de los predictores de nivel 2
Ej: Enders & Tofighi Tabla 2, ver ajuste de predictor de tamaño (SIZE) cuando HOURS es CGM en lugar de CWC
3. Predictores en ambos niveles
Caso de modelos contextuales o composicionales
Requiere usar los puntajes individuales y los promedios de los clusters
Por lo tanto se requiere descomponer la varianza de la pendiente en within y between,
El objetivo es saber si γ01 es significativo y distinto de γ10, es decir, si hay un efecto del grupo más allá del efecto individual
Al estar presentes los promedios de los clusters, γ10 es equivalente para ambos centrados (CGM=CWC), ya que CGM se encuentra parcializado de los promedios grupales
Por lo tanto, dos vías equivalentes para evaluar esto:
CWC: restar ambos coeficientes y ver si la diferencia es significativa
CGM: si γ01 es significativo implica que la diferencia es significativa
Para el caso de CWC: γ10−γ01=−.608−.294=.315
Para CGM: γ01=.315 (equivalente a la diferencia con CWC), y es significativo.
4. Interacción entre niveles
La estimación CGM de γ11 (coeficiente de interacción) es una mezcla poco interpretable de interacciones a ambos niveles
CWC desacopla las interacciones
Por lo tanto, se recomienda CWC en interacciones entre niveles
Resumen
un predictor nivel 1 no centrado contiene elementos de varianza entre y dentro
por lo tanto, se requiere separar ambas varianzas según las hipótesis a contrastar
en general, para hipótesis de nivel 1 los predictores deben estar centrados al grupo, o controlados por el promedio del predictor por clusters como variable de nivel 2
centardo es de especial relevancia al establecer hipótesis de interacciones entre niveles
Modelos multinivel
